Nam's Blog
IMO 2023 Problem 5
Let \(n\) be a positive integer. A Japanese triangle consists of \(1 + 2 + \dots + n\) circles arranged in an equilateral triangular shape such that for each \(i = 1\) , \(2\) , \(\dots\) , \(n\) , the \(i^{th}\) row contains exactly \(i\) circles, exactly one of which is coloured red. A ninja path in a Japanese triangle is a sequence of \(n\) circles obtained by starting in the top row, then repeatedly going from a circle to one of the two circles immediately below it and finishing in the bottom row. Here is an example of a Japanese triangle with \(n = 6\) , along with a ninja path in that triangle containing two red circles.
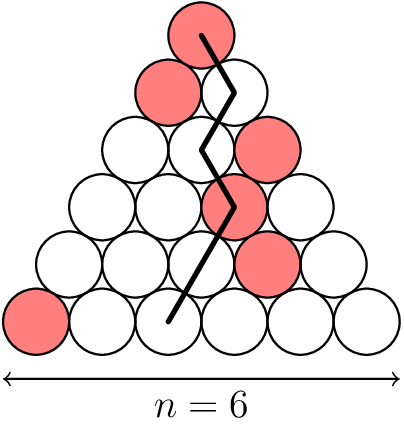In terms of \(n\) , find the greatest \(k\) such that in each Japanese triangle there is a ninja path containing at least \(k\) red circles.
IMO 2023 Problem 4
Problem 4: Let \(x_1,x_2,\dots,x_{2023}\) be pairwise different positive real numbers such that
\[a_n=\sqrt{(x_1+x_2+\dots+x_n)\left(\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_n}\right)}\]is an integer for every \(n=1,2,\dots,2023.\) Prove that \(a_{2023} \geqslant 3034.\)
Hint: Motivation. It is obvious to see that \(3034=2022\times\frac 32+1,\) which leads us to the lemma below \(.\)
Read more »IMO 2023 Problem 3
Problem 3: For each integer \(k \geqslant 2\), determine all infinite sequences of positive integers \(a_1, a_2, \ldots\) for which there exists a polynomial \(P\) of the form \(P(x)=x^k+c_{k-1} x^{k-1}+\cdots+c_1 x+c_0\), where \(c_0, c_1, \ldots, c_{k-1}\) are non-negative integers, such that
\[P\left(a_n\right)=a_{n+1} a_{n+2} \cdots a_{n+k}\]for every integer \(n \geqslant 1\).
Read more »IMO 2023 P1
Question: Determine all composite integers \(n>1\) that satisfy the following property: if $$d_1, d_2, \ldots, d_k$$ are all the positive divisors of \(n\) with \(1= d_1 < d_2< \cdots < d_k = n\), then \(d_i\) divides $$d_{i+1}+d_{i+2}$$ for every \(1 \leqslant i \leqslant k-2.\)
Read full article here .
Read more »How can we write a formula in file md 3?
How can we write a formula in file md?
We can write a formula in file md similar to write in tex. The formula $x^2+1=0$ can be seen clearly in file md, but when we see this post on website it no longer appear like that.
Read more »