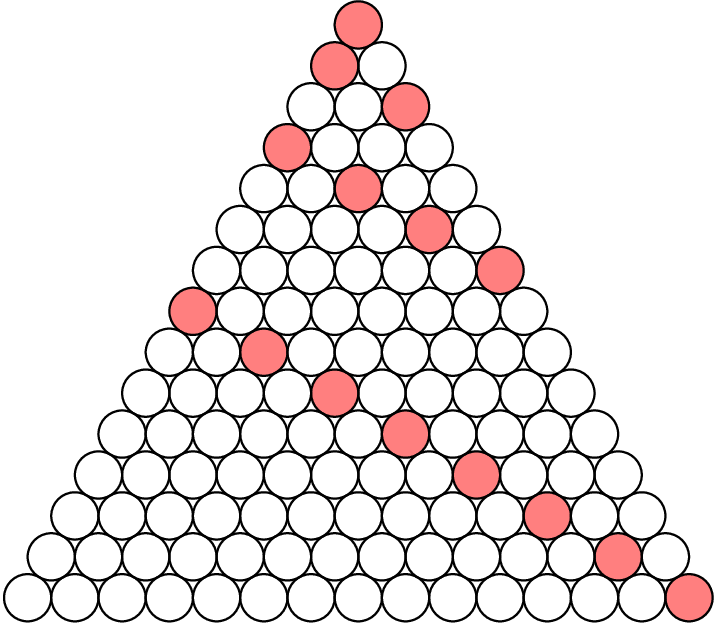
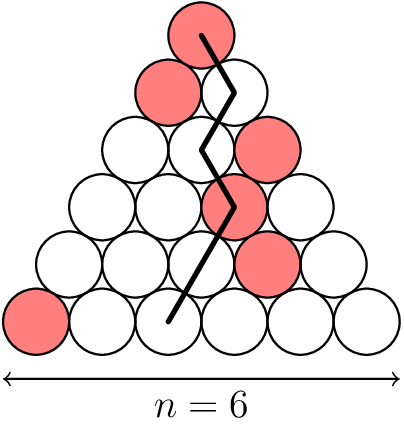
Let \(n\) be a positive integer. A Japanese triangle consists of \(1 + 2 + \dots + n\) circles arranged in an equilateral triangular shape such that for each \(i = 1\) , \(2\) , \(\dots\) , \(n\) , the \(i^{th}\) row contains exactly \(i\) circles, exactly one of which is coloured red. A ninja path in a Japanese triangle is a sequence of \(n\) circles obtained by starting in the top row, then repeatedly going from a circle to one of the two circles immediately below it and finishing in the bottom row. Here is an example of a Japanese triangle with \(n = 6\) , along with a ninja path in that triangle containing two red circles.
In terms of \(n\) , find the greatest \(k\) such that in each Japanese triangle there is a ninja path containing at least \(k\) red circles.
Solution 1. The answer is \(\left \lfloor \log_2 n \right \rfloor + 1\) . For convenience, we label the rows of the triangle from the top, starting the count from \(1\) . For each red circle \(A\) , we assign it a number corresponding to the maximal amount of red circles that can appear in a ninja path from the top of the triangle to \(A\) . We can see that in a Japanese triangle, there is a ninja path with \(t\) red circles iff there is a red circle assigned with the number \(t\) . We are left to find the maximum number \(k\) that can appear in any Japanese triangle.
Claim 1: If \(A,B\) get assigned by the same number \(t\) , then the sub-triangle with \(A\) as the top can not contain \(B\) and vice versa.
Proof: Kinda straightforward. If the sub-triangle with \(A\) as the top contains \(B\) , then there is a ninja path that goes to \(A\) , and then \(B\) , with at least \(t+1\) red triangles, and \(B\) can not be assigned the number \(t\) .
Claim 2: there are at most \(2^i\) red circles assigned with the number \(i\) .
Proof: We proceed by induction. \(i=1\) is trivial. Assume that for any \(i \le t\) , there are at most \(2^i\) red circles assigned with the number \(i\) . Then, there are at most \(2^{t+1}-1\) red circles assigned with a number less than or equal to \(t\) . Hence, there exists a red circle \(A\) assigned with the number \(t+1\) that lies in a row \(h \le 2^{t+1}\) . By Claim 1, the sub-triangle with \(A\) as the top can not contain any other red circles with the number \(t+1\) . It also means that there are at most \(2^{t+1}-1\) rows either oriented “/” or “" that can contain a red circle of number \(t+1\) . By Claim 1 again, each of these rows can have at most one red circle with the number \(t+1\) . So there can be at most \(2^{t+1}\) red circles assigned with the number \(t+1\) , proving the induction.
The rest of the problem should be straightforward. Due to Claim 2, there is always a red circle assigned with the number \(\left \lfloor \log_2 n \right \rfloor + 1\) in any Japanese triangle with \(n\) rows. Using the similar idea, we can also construct a Japanese triangle where the maximal number assigned to a red circle is \(\left \lfloor \log_2 n \right \rfloor + 1\) . Hence, \(\left \lfloor \log_2 n \right \rfloor + 1\) is the maximal number. \(\square\)
Solution 2 Let’s denote the circles as \((x,y)\) - the \(y\) th circle on the \(x\) th row, and let \(f(x,y)\) denote the most red we can visit in a path finishing in \((x,y)\) . We observe that adding a new row means that \(f(x,y) = \max(f(x-1,y-1),f(x-1,y))\) , and we need to find the smallest possible value of the largest number on the \(n\) th row.
Claim: On row \(2^z\) , we have a circle with \(f \geq z+1\) , and the sum of all \(f\) is at least \(z \cdot 2^z + 1\) .
We will prove this by induction:
Base: \(n=1\) and \(n=2\) \(\Rightarrow\) OK
Induction step: WLOG(let the largest \(f\) on row \(2^z\) be \((2^z,1)\) ). Adding \(2^z\) rows means that \(f(2^{z+1},i) = z+1\) , where \(i\) is from \(1\) to \(2^z+1\) . (If \(f(2^{z+1},i) \geq z+2\) , then the induction is done.) The rest have a sum of at least \((z \cdot 2^z - z) + 2^z\) (We add \(2^z\) because we have added that many rows, and each row we add, we increase the sum of a \(f\) by \(1\) because of a red circle).
But by pigeonhole principle, we have \(2^z-1\) numbers with a sum of \((z+1) \cdot 2^z - z = (z+1) \cdot (2^z-1) + 1\) , which means at least one circle has \(f \geq z+2\) . Then, the sum of all the circles on row \(2^{z+1}\) is at least \((z+1) \cdot (2^z-1) + 1 + (z+1) \cdot (2^z+1) = (z+1) \cdot 2^{z+1} + 1\) , which satisfies the induction.
Note: If we ever get \(f \geq z+2\) earlier, then the same logic applies, and the sum still ends up \(\geq (z+1) \cdot 2^{z+1} + 1\) .
This means for row \(n\) , we know the answer is \(\geq \left\lfloor \log_2(n) \right\rfloor +1\) . The example below shows that the answer can’t be \(\geq \left\lfloor \log_2(n) \right\rfloor +2\) , so it’s \(\boxed{\left\lfloor \log_2(n) \right\rfloor + 1}\)
